アクセスいただき、ありがとうございます。MENSA(メンサ)合格者の「たまご」です。
当ブログでは、世の中に少ないMENSA(メンサ)の情報を、私の経験と感想を交えてご紹介しています。
MENSA(メンサ)情報は、全8ページから構成されています。
ご興味のあるところから覗いていただきつつ、是非すべてのページを読破いただけますと幸いです!

この記事はNo.3です


<プロフィール>
- ごくごく一般的な会社員
- 2018年2月にMENSA合格
- クイズ番組は結構好き
- コロナ禍にブログを開始
はじめに


私が調べた限りでは、ルーマニアメンサは問題のみ公開されており、解答・解説を見つけることができませんでした。以下で紹介する解答・解説は私の個人的見解である点をご了承ください。(明らかな誤りがあるようでしたら、TwitterのDMにてお知らせいただけますと幸いです)



さあ、解いてみよう!
オンラインテスト実施時の注意事項


せっかくの機会ですので、少しでも本番に近い緊張感を持って臨みましょう!
- 制限時間は10分間
- 問題数は24問
- タイマーを用意



準備ができたら、スタート!
メンサ:問題と解説(No.1~4)


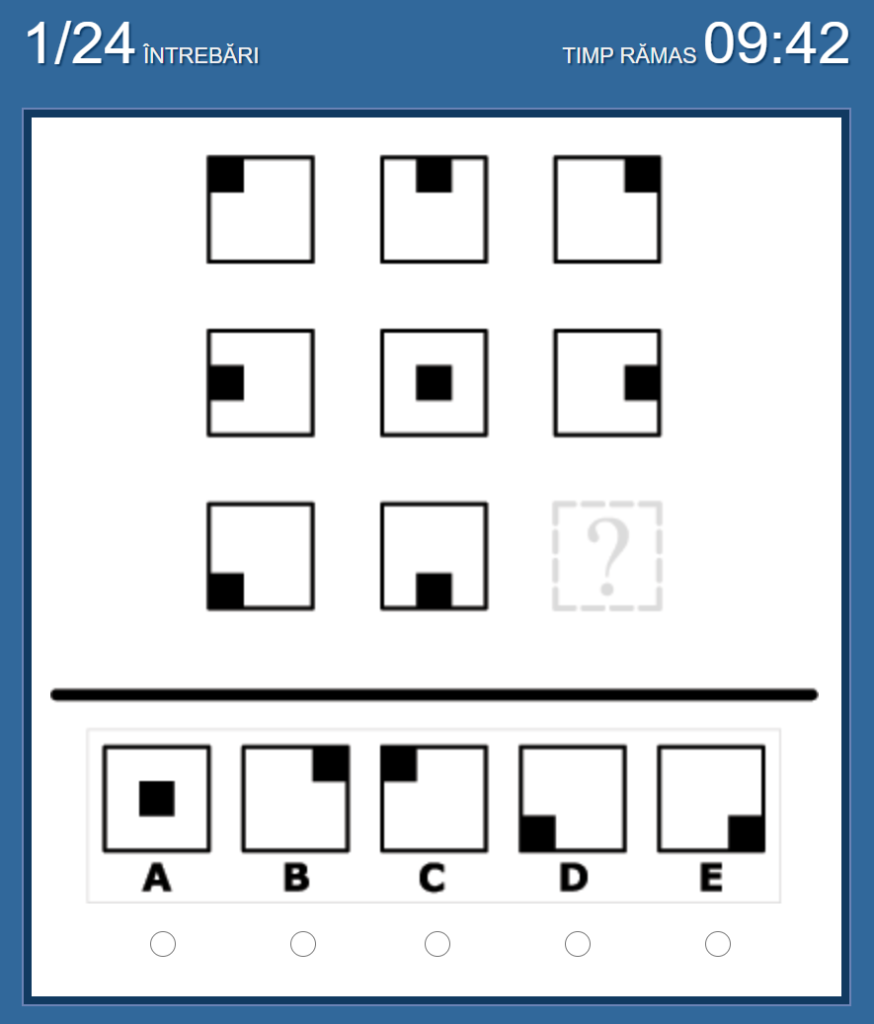



No.1 私の答えは「E」
図形が右に行くごとに、黒い正方形も右に移動していく、という法則。
No.2 私の答えは「C」
同じ図形が3つずつ存在する、という法則。
「田」の図形だけ2個しかない。
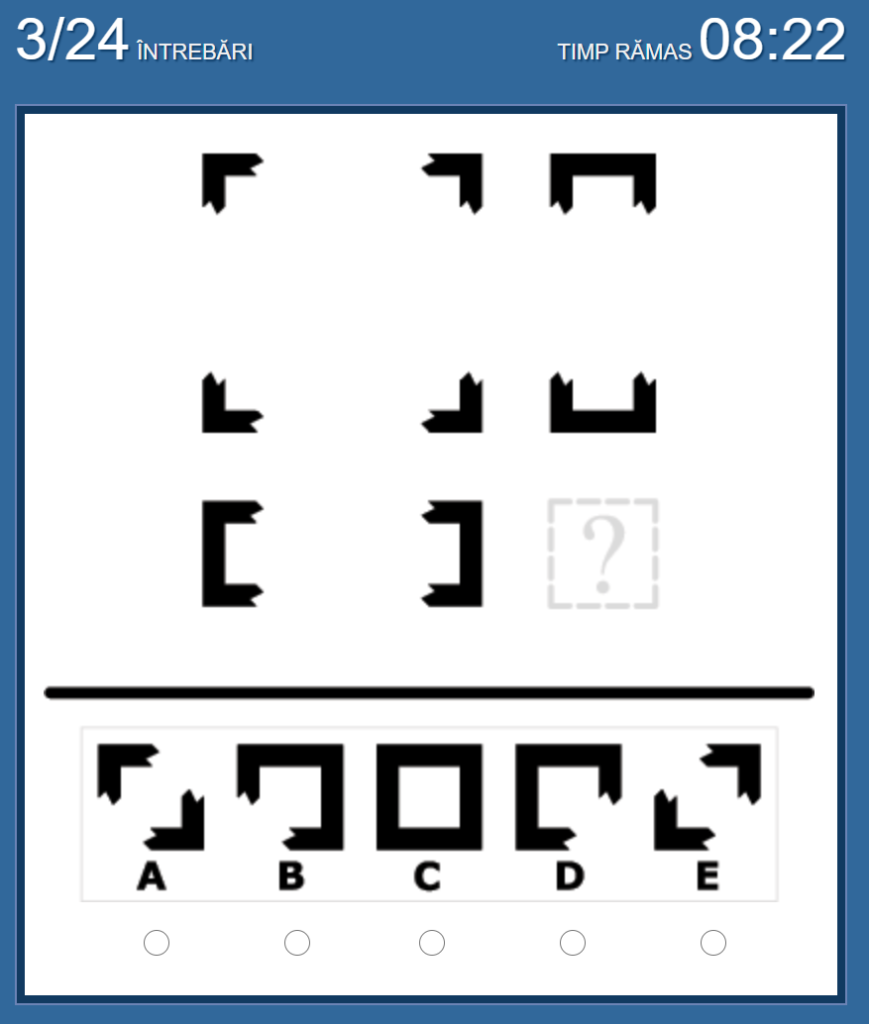


No.3 私の答えは「C」
「左の図形」+「真ん中の図形」=「右の図形」になる、という法則。
[+]= □ ←イメージ
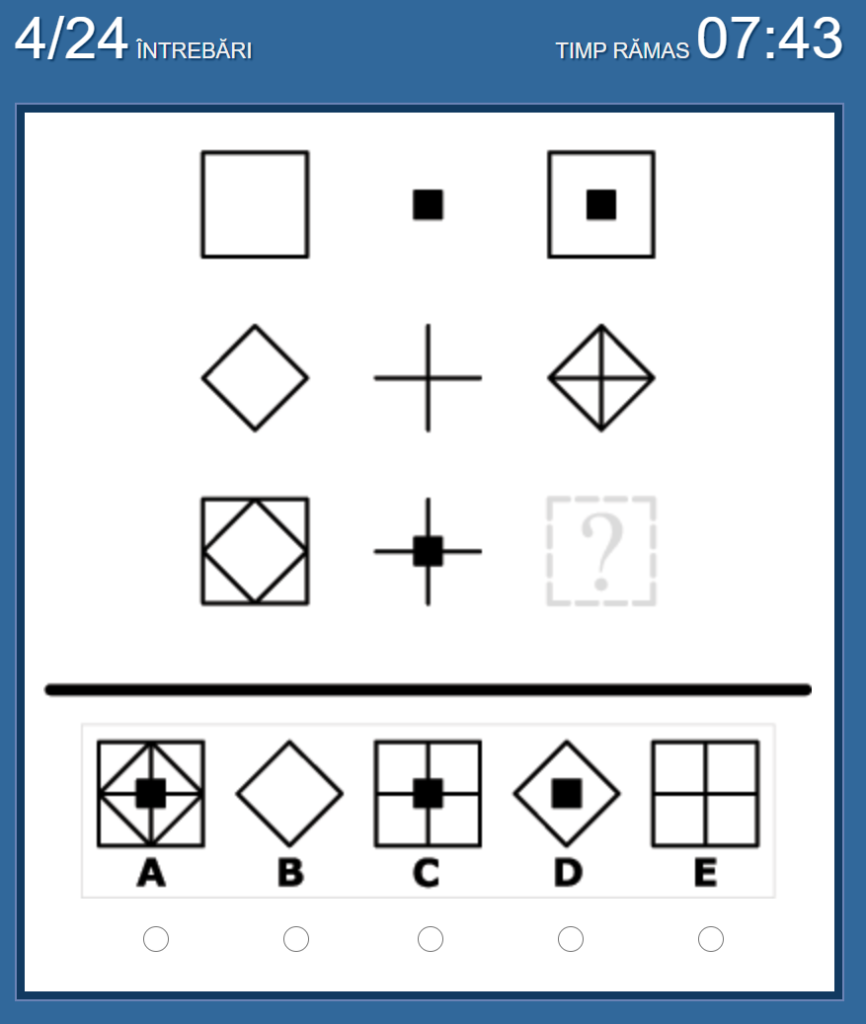
No.4 私の答えは「A」
No.3と同じ考え方。
メンサ:問題と解説(No.5~8)


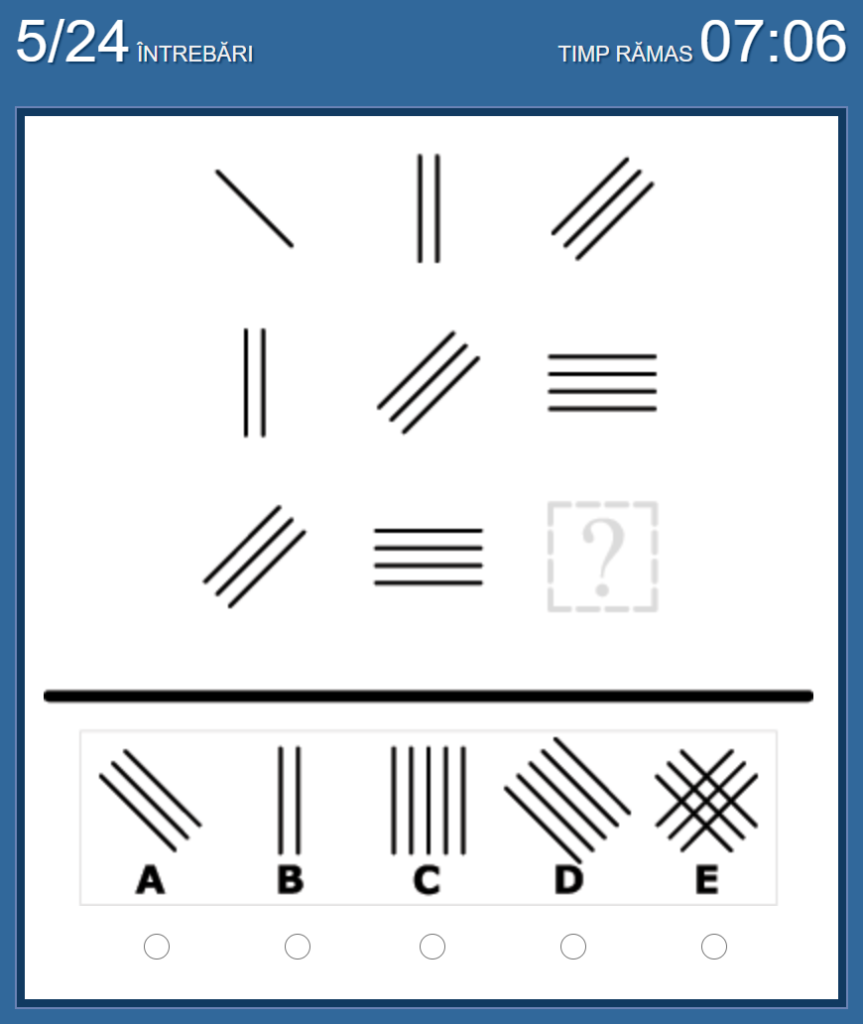

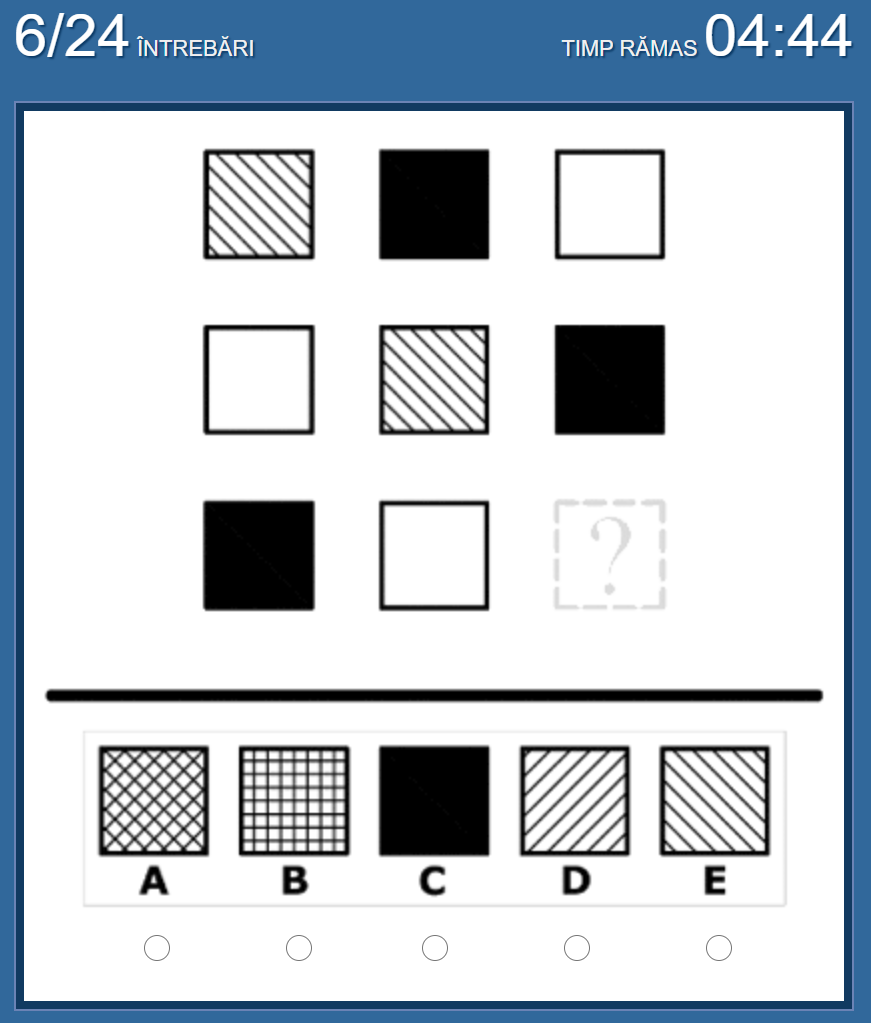

No.5 私の答えは「D」
図形が右に行くごとに、時計回りに45度回転しつつ、棒の本数が増えていく、という法則。
(3本(右上斜め)→4本(真横)→5本(右下斜め)=「D」が答え)
No.6 私の答えは「E」
先述のNo.2と同じ考え方。Eの図形だけ、2個しかない。
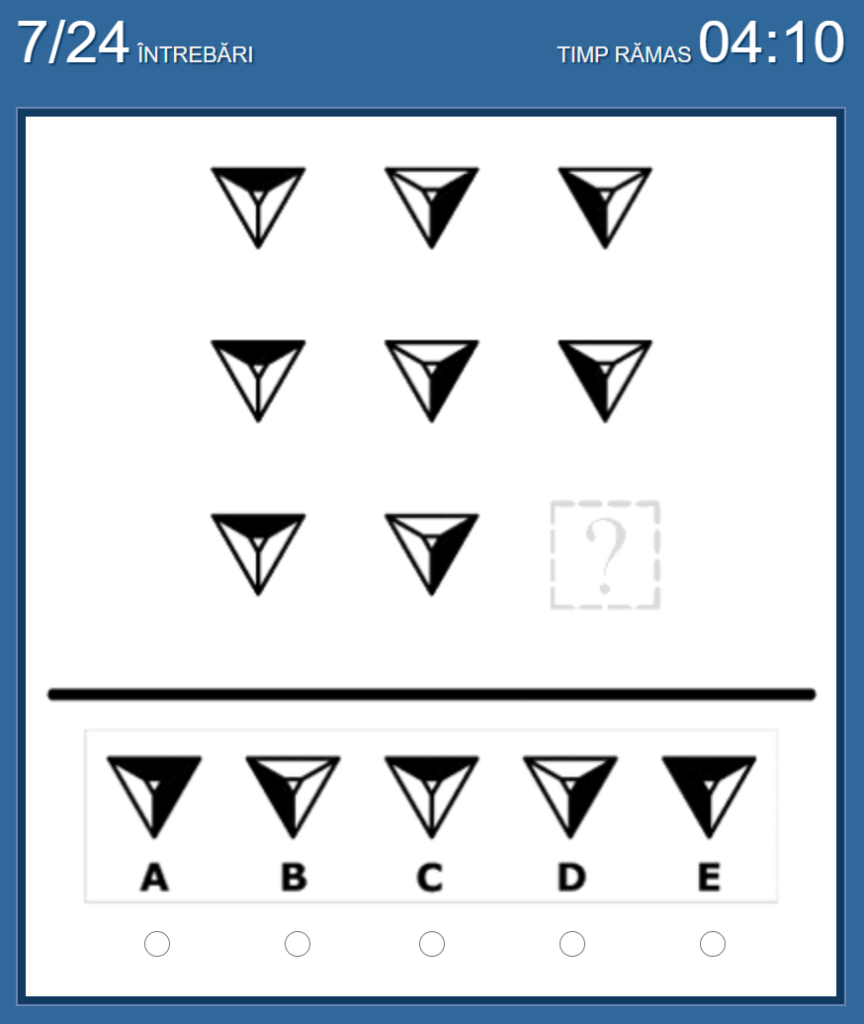


No.7 私の答えは「B」
各列、同じ図形が縦に並ぶ、という法則。
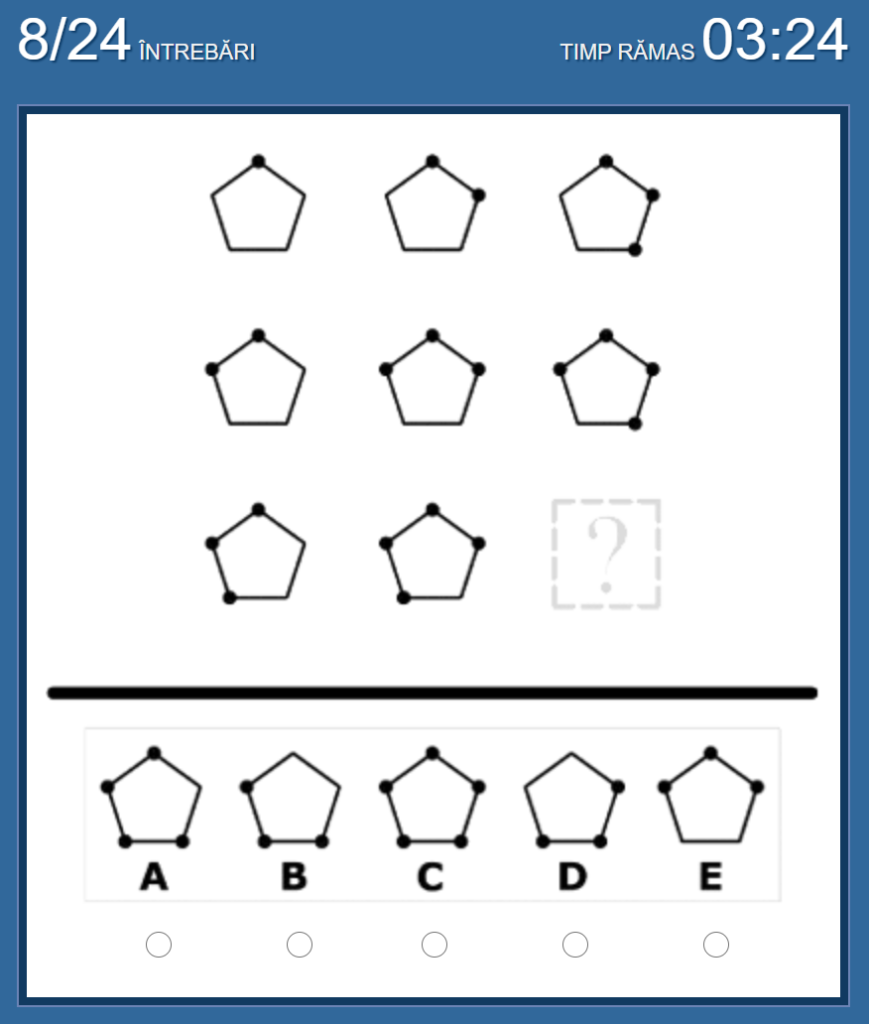
No.8 私の答えは「C」
図形が右に行くごとに、右に黒ポチが増えていく、という法則。
(黒ポチ3つ→黒ポチ4つ→黒ポチ5つ=「C」が答え)
メンサ:問題と解説(No.9~12)


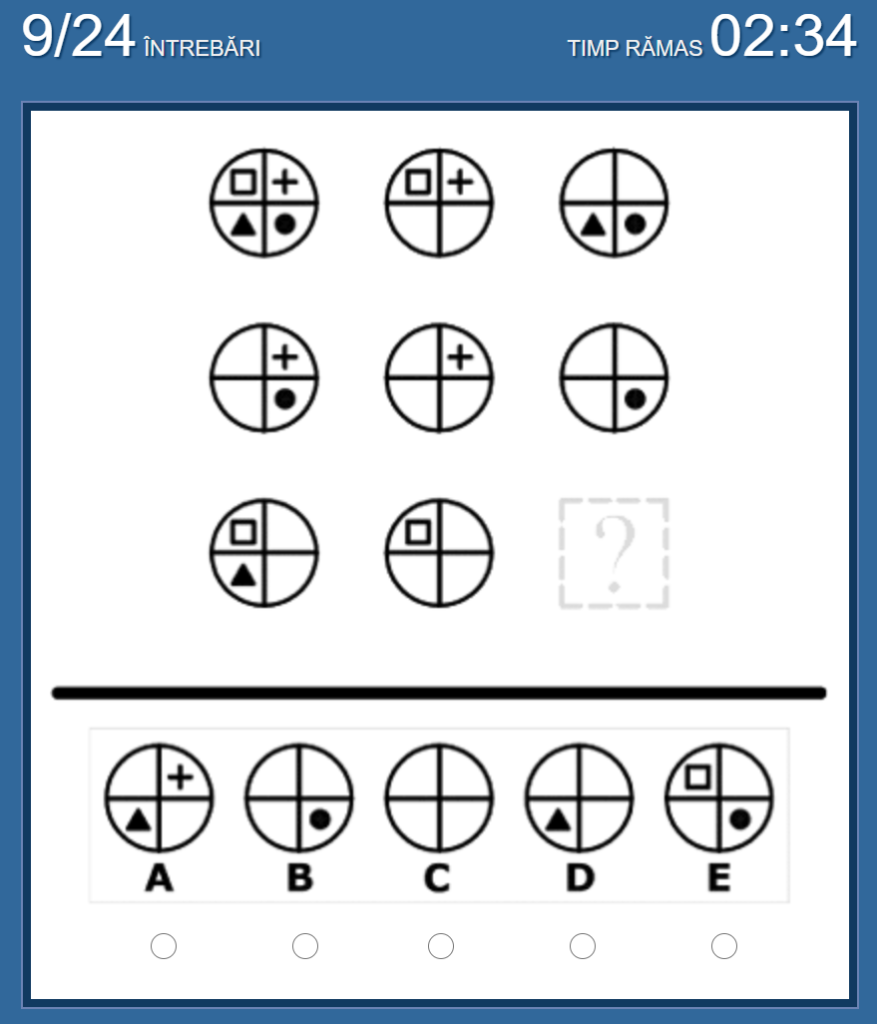



No.9 私の答えは「D」
「左の図形」-「真ん中の図形」=「右の図形」になる、という法則。
□▲-□=▲ なので、「D」が答え。
No.10 私の答えは「B」
各図形および各柄が3つずつ存在する、という法則。
(図形ではマルが1つ足りていない。柄では斜線が1つ足りていない。従って「B」が答え。)
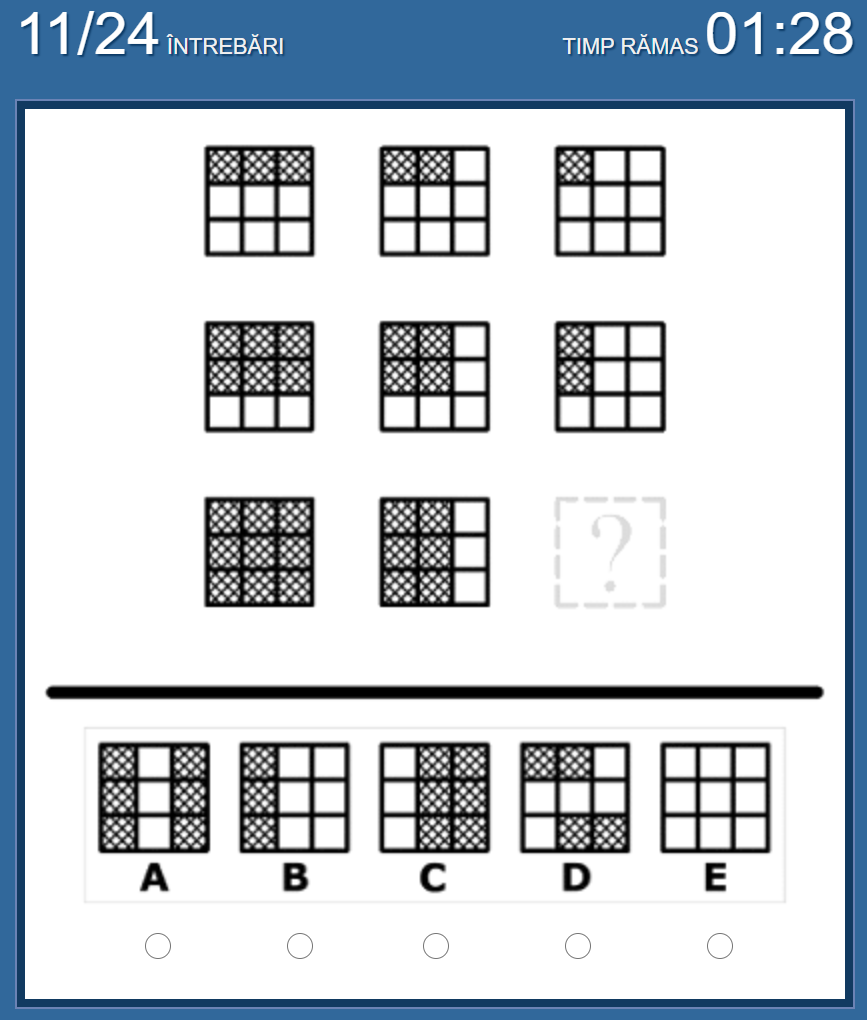


No.11 私の答えは「B」
図形が右に行くごとに、黒色の右列が白色になっていく、という法則。
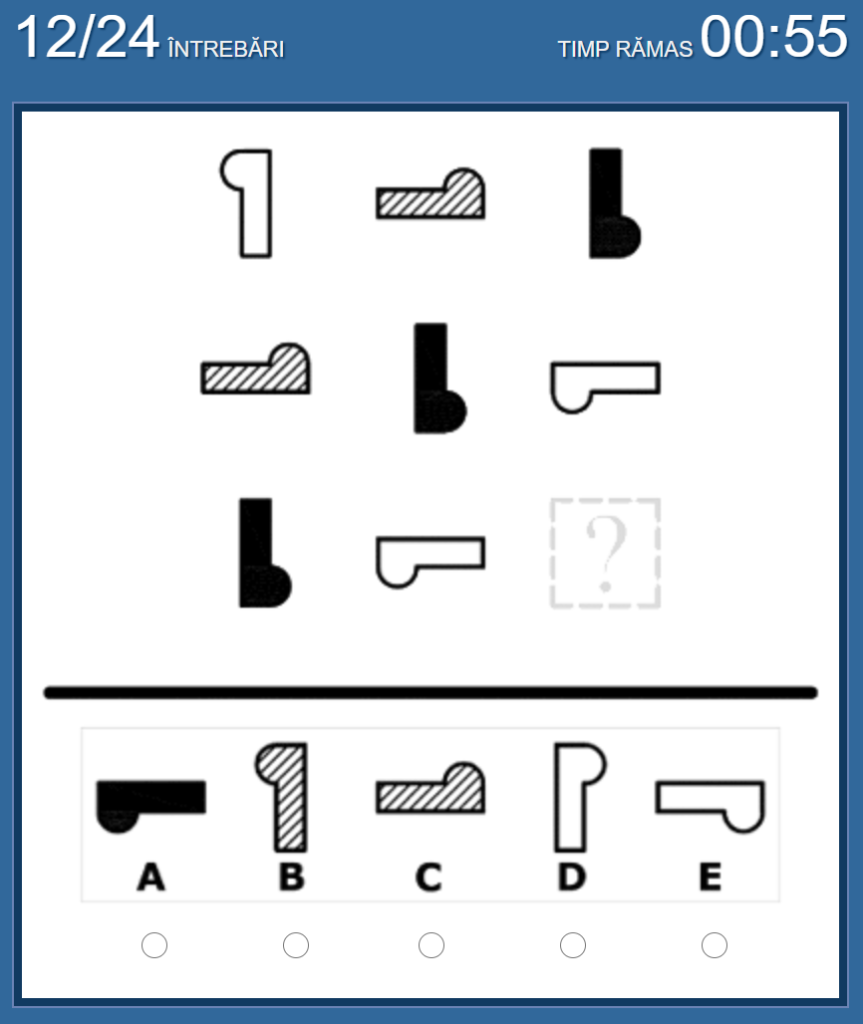
No.12 私の答えは「B」
図形が右に行くごとに、時計回りに90度回転。また各行には3種類の柄が存在している、という法則。
メンサ:問題と解説(No.13~16)


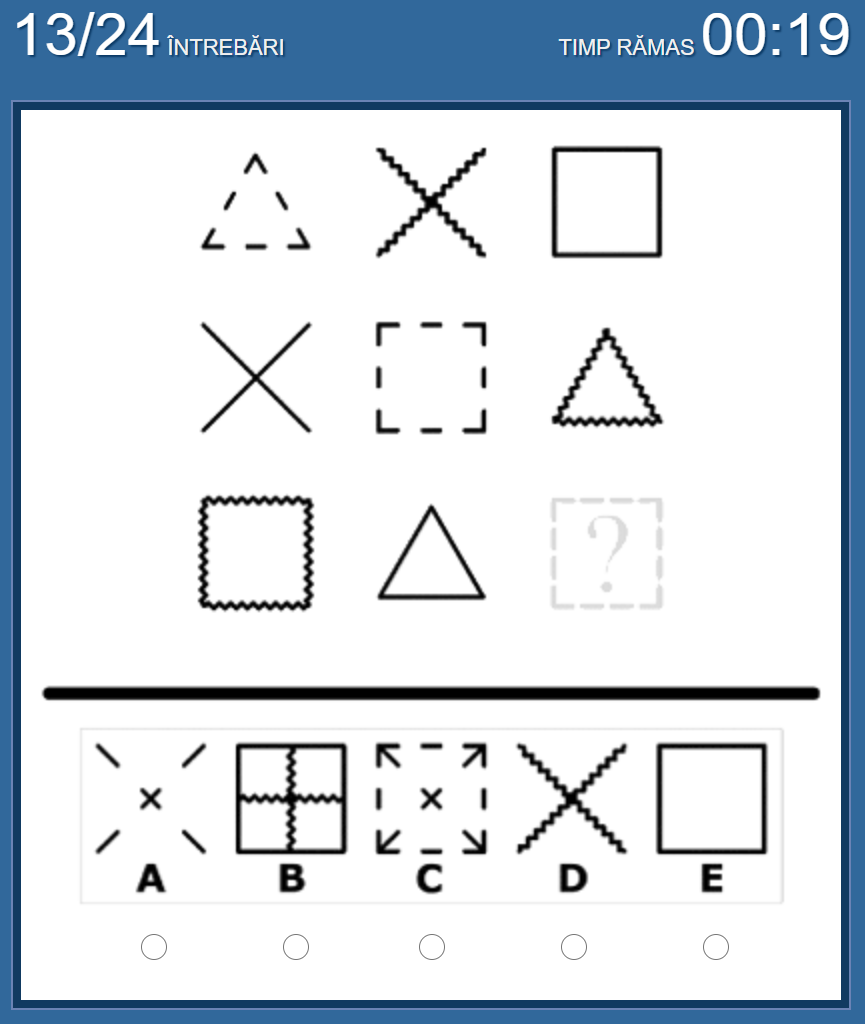


No.13 私の答えは「A」
各図形および各柄が3つずつ存在する、という法則。
「点線」の「バツ(×)」がないので、「A」が答え。
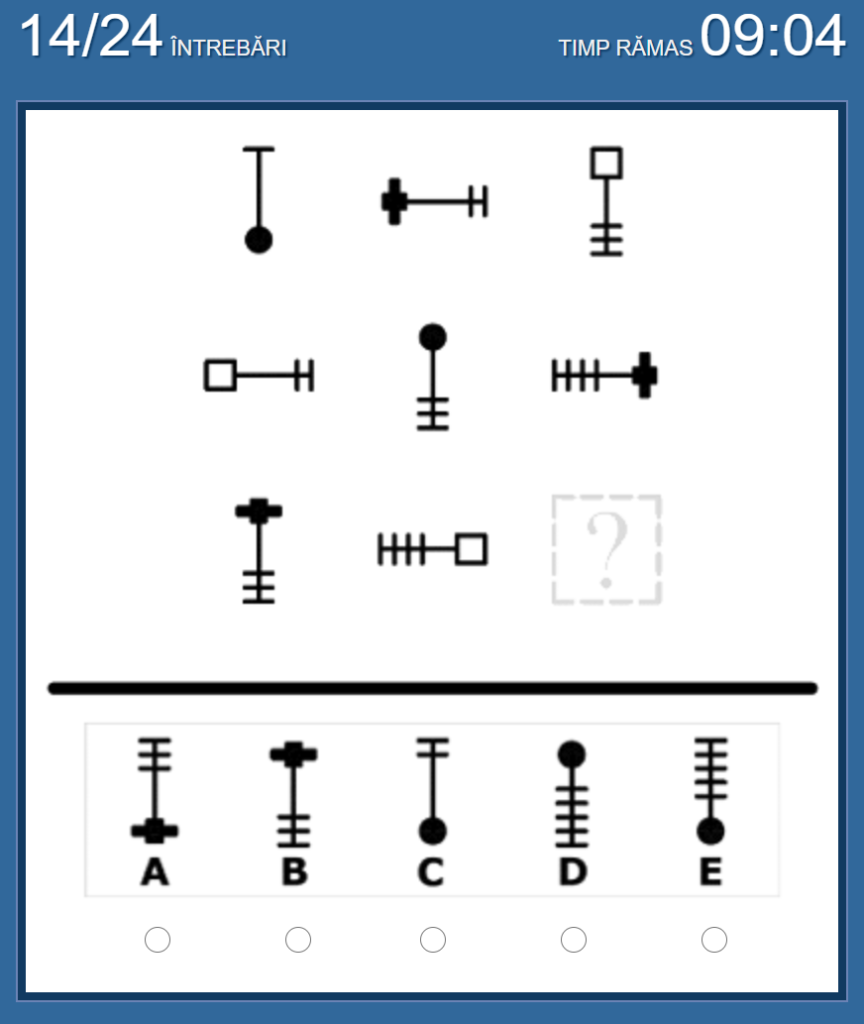
No.14 私の答えは「E」
図形が右に行くごとに、①時計回りに90度回転、②横棒の本数が1本ずつ増えていく、③各行3種類の図形が存在する、という法則。 ①については上→右→「下」、②については3→4→「5本」、③については足りない図形は「黒丸(●)」。従って「E」が答え。
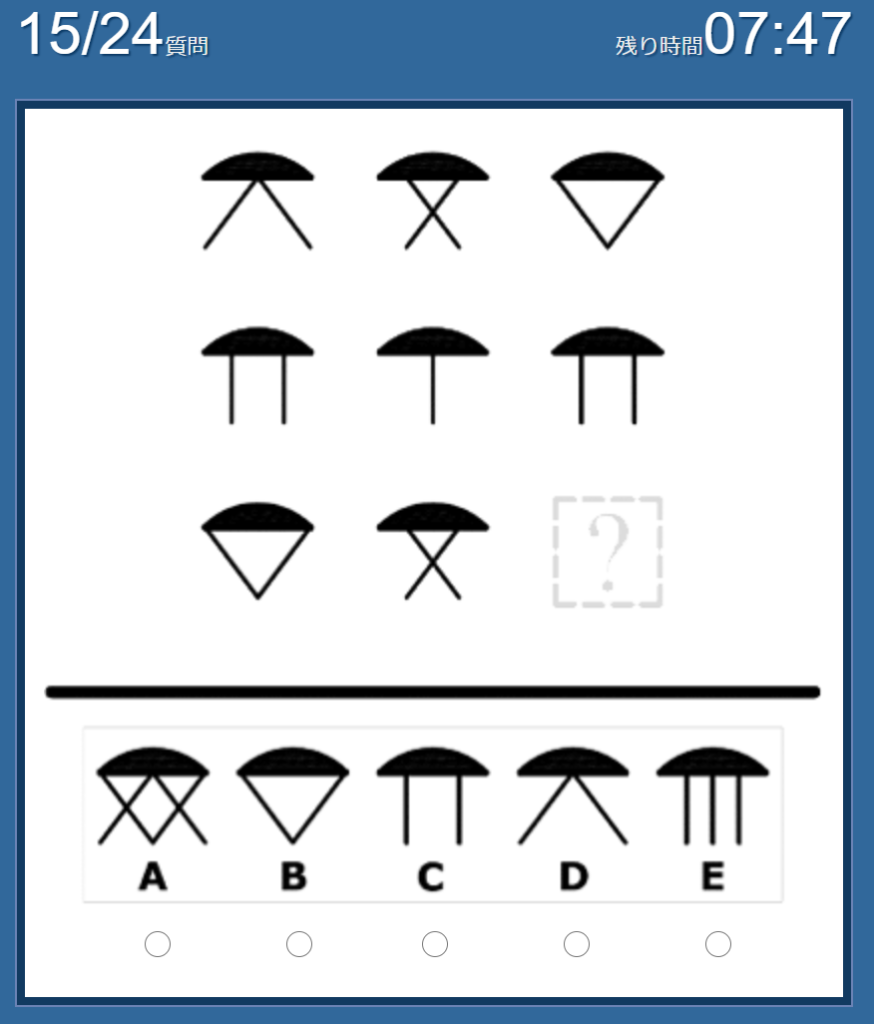

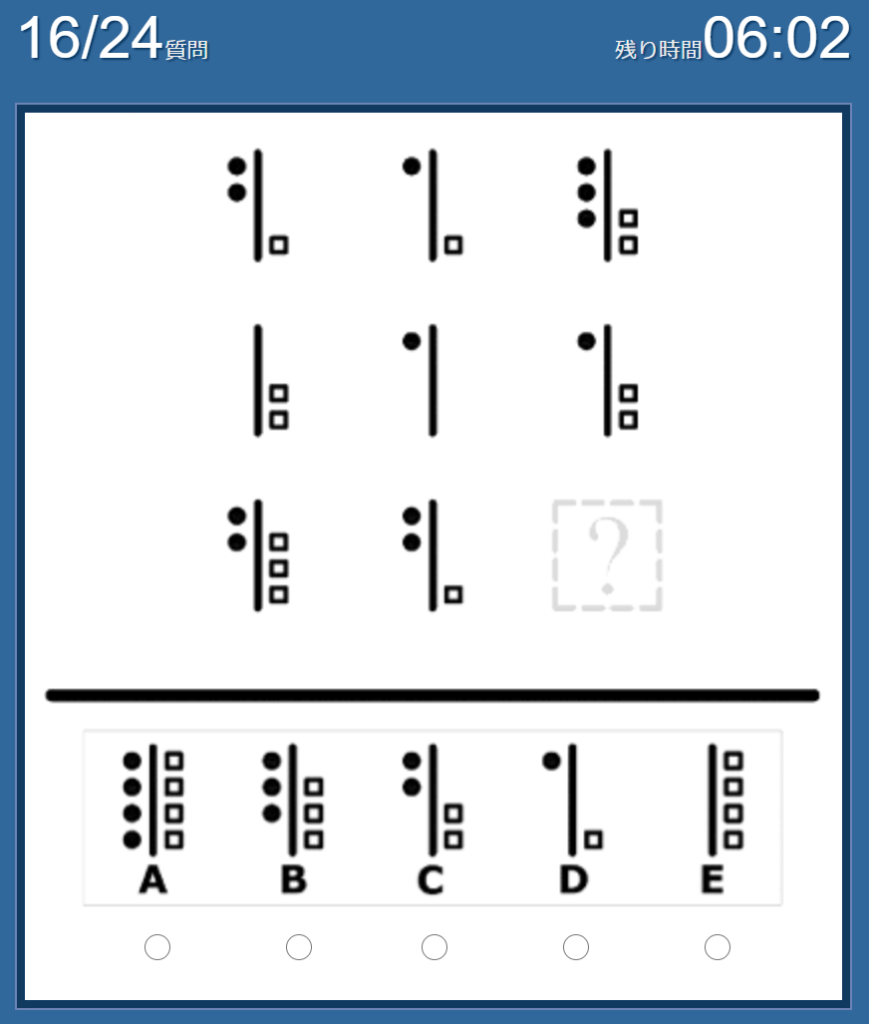

No.15 私の答えは「D」
中心を起点として、4種類の図形が2個ずつ存在している、という法則。
足りないのは「D」の図形。(中心の図形は、起点として存在しているだけ)
No.16 私の答えは「A」
「左の図形」+「真ん中の図形」=「右の図形」になる、という法則。
黒丸(●)は、2+2=4
四角(□)は、3+1=4
メンサ:問題と解説(No.17~20)






No.17 私の答えは「A」
図形が右に行くごとに、風車の羽が1枚ずつ欠けていく、という法則。
羽が2枚→羽が1枚→「羽が無い」=「A」が答え。
No.18 私の答えは「A」
図形が右に行くごとに、①マル(〇)が時計回りに移動し、②太線は反時計回りに移動する、という法則。
①については右→左→「上」、②については左→右→「上」。従って「A」が答え。
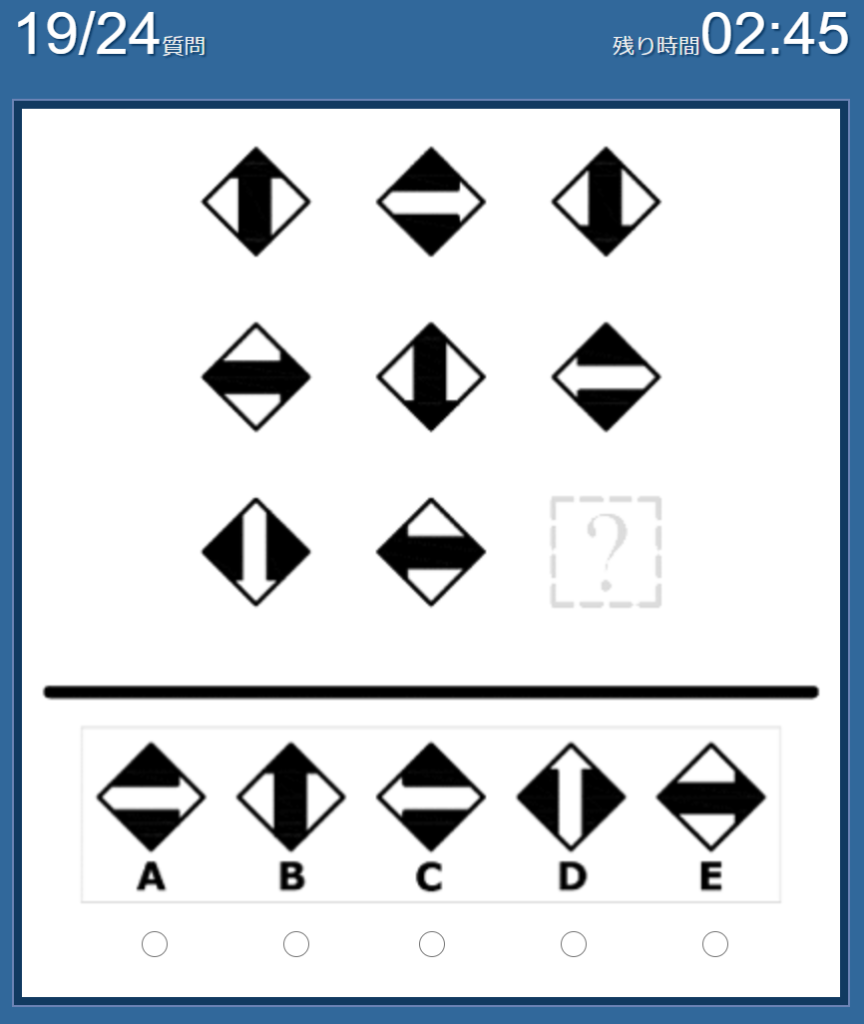



No.19 私の答えは「B」
図形が右に行くごとに、①矢印が時計回りに移動し、②各行に「黒い矢印が2本・白い矢印が1本」存在する、という法則。
①については下→左→「上」、②については黒い矢印が足りない。従って「B」が答え。
No.20 私の答えは「E」
「左の図形」+「真ん中の図形」=「右の図形」になる、という法則。
メンサ:問題と解説(No.21~24)


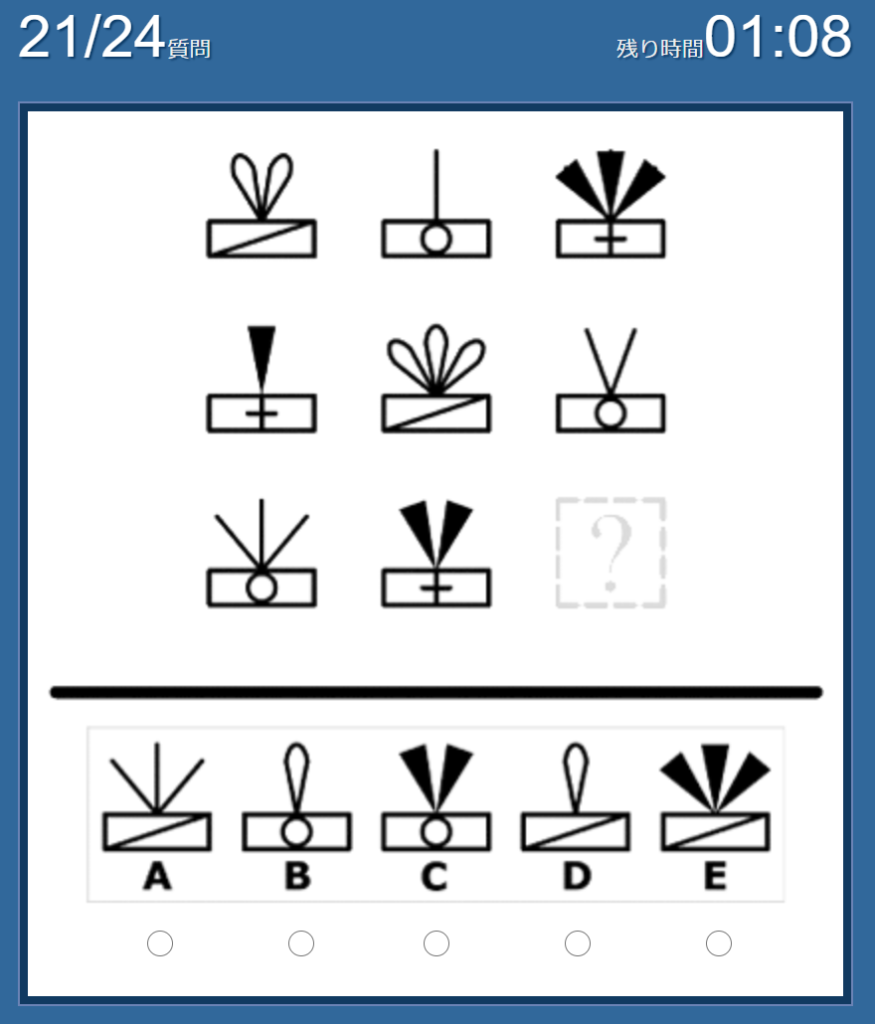


No.21 私の答えは「D」
各行の図形には①3種類の飾り(プレゼントのリボンのようなもの)があり、②飾りの本数がそれぞれ異なっており「1or2or3」、③箱の中のマークも3種類存在している、という法則。
①について、候補となる飾りは「B or D」。②について、3本→2本→「1本」となり、未だ候補は「B or D」のまま。③足りない図形は斜線。従って「D」が答え。
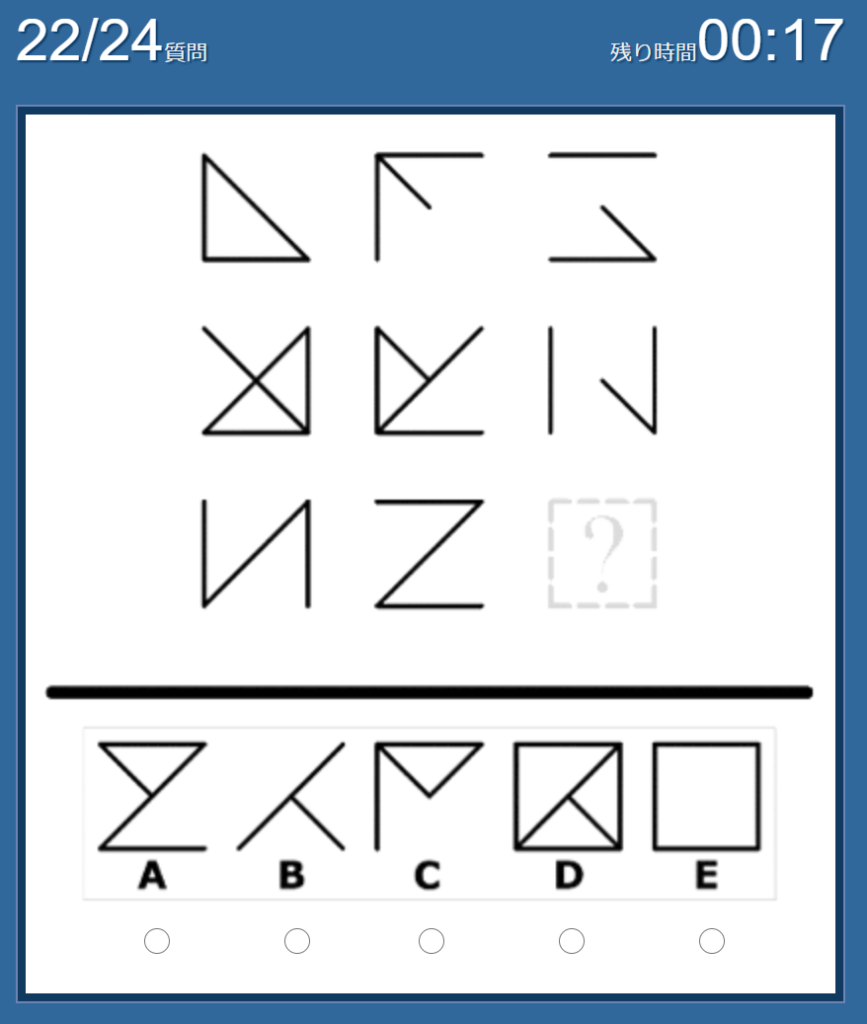
No.22 私の答えは「E」
「左の図形」+「真ん中の図形」-「重なり合っている部分」=「右の図形」になる、という法則。
3行目の図形(2つ)を重ね、重なり合っている部分(斜線)を除くと、四角が完成するので「E」が答え。




No.23 私の答えは「D」
図形が右に行くごとに、①頭の色が変わっていく、②胴体の色は変わらない、③足の形も変わっていく、という法則。
①について、まだ使われていない色は「白」。②については「網掛け」。③について、まだ使われていないのは土偶みたいな形。従って「D」が答え。
No.24 私の答えは「C」
「左の図形」+「真ん中の図形」-「重なり合っている部分」=「右の図形」になる、という法則。
3行目の図形(2つ)を重ねてみると、重なり合っていないのは「中央のマル」と「右上の三角」のみ。
従って「C」が答え。
ルーマニアメンサ(オンラインテスト)結果発表
24問、お疲れさまでした!
集中して解くと、あっという間だったのではないでしょうか。
すべての回答を終えると、IQ値のゾーンが表示されます。(下図)


Google翻訳によると、次のことが書かれています。
おめでとうございます!このテストで得られる最高の結果となりました!
人口のわずか4%が、126以上のIQを持っています。
MENSAの一員となるには、131以上のIQが必要であり、これは人口の2%に相当します。
あなたはMENSAの資格を得る可能性が高いです。
MENSAのテストに申込んで確認してみてください!
巷では、「MENSA(メンサ)合格には、IQ130以上が必要」と言われていますので、このコメントを読む限り、その説は正しそうですね。
ルーマニアメンサにおいては、上図がMAX値と思われます。
皆さまのお手元には、どのようなグラフが表示されたでしょうか ^ ^



繰り返し練習あるのみ!
\ もっと問題を解きたい方へ /
メンサ関連図書







